子集问题：阶乘之和

题目

来自 XMUT 老 oj 平台的一道题：

Description

给你一个非负数整数N，判断N是不是一些数（这些数不允许重复使用，且为正数）的阶乘之和，如9=1!+2!+3!，如果是，则输出Yes，否则输出No

Input

第一行有一个整数M（0 < M < 100）表示有M组测试数据；
每组测试数据有一个正整数N（0 < N <= 100000）；

Output

如果符合条件，输出Yes，否则输出No;

Sample Input

3
24
29
31

Sample Output

Yes
No
Yes

题解

看似题目很简洁，好像很容易的样子（是我轻敌了……），实际上我花了一个半小时才 AC 了这道题…… 首先题目最头疼是要把所有子集求出来。求子集有递归回溯和二进制掩码两种方法，因为二进制有些许门槛（位运算），所以我选择了用递归回溯。
递归回溯挺像分叉树的数据结构。
如图，有 4 个数据的结构通过递归可以穷举所有可能性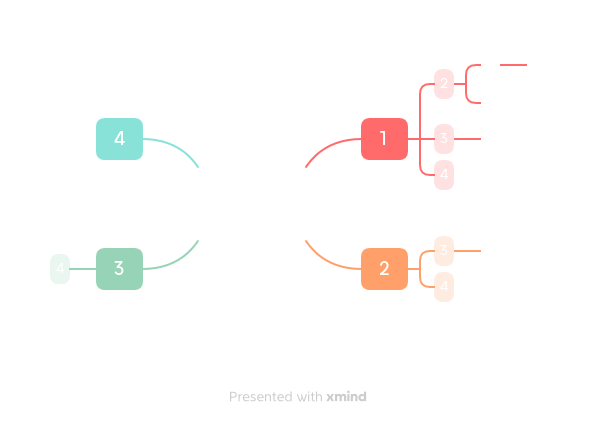：通过递归链可以穷举出所有的子集而不重复。对每个阶乘项子集求和与目标值比对就可以得到答案。

数据量

题目的数据量还行：

第一行有一个整数M（0 < M < 100）表示有M组测试数据；
每组测试数据有一个正整数N（0 < N <= 100000）；

这种要暴力穷举的题目常常会因为复杂度而无法通过，对于阶乘，其增长幅度是很快的。比如题目中的 N 最大为 $10^{5}$，而阶乘到 9 就已经达到 362880，所以我们用来打表的阶乘表只需要 10 个就足以，当然可以多一点点也没事。不过学校的平台给的内存很充裕，我直接把数组给了 1005 位。

阶乘表

我们需要一个阶乘表，该阶乘表要满足在大小为 1 ~ N 的阶乘。我们使用整形 n 来存储测试数据个数，用整形 target 来存储该数据。显然对于任意测试数据打表，以下逻辑足以：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


int fac = 1, target;
int list[M];
scanf("%d", &target);
for (j = 1; fac <= target; j++)
{
    fac *= j;
    list[j - 1] = fac;
}
if (fac == target)
{
    printf("Yes\n");
    break;
}

其中 M 是一个常数，通过的代码是 1005。
这里的 j 还可以在后面作为阶乘表的长度带入递归函数中。

穷举子集，求和判断

这里就要开始构造递归函数了。该函数的形参需要的还蛮多，其声明如下：

1

int recall(int list[], int len, int StartIndex, int sum, int target);

各参数作用:

int list[] 阶乘表
int len 阶乘表长度
int StartIndex 递归起始下标
int sum 求和参数
int target 目标值

在最初调用该递归时候其参数为:

1

recall(list, j, 0, 0, target);

这里先把整个递归函数放出来：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


int recall(int list[], int len, int StartIndex, int sum, int target)
{
    int i;
    if (sum == target)
        return 1;
    if (StartIndex >= len || sum > target)
        return 0;
    for (i = StartIndex; i < len; i++)
        if (recall(list, len, i + 1, sum + list[i], target))
            return 1;
    return 0;
}

在函数头声明 i 是因为学校 oj 过于奇葩，GCC 在 if 语句内声明直接编译错误

在每次递归时候都要对求和参数 sum 和目标值 target 作相等性判断，如果相等就返回 1，而后不断退栈。

1
2


if (sum == target)
    return 1;

但是在最开始还是需要进行判断返回的。这也是后面 for 语句下做的事情。
当递归到深度超过阶乘表的长度时就不能再继续递归了，不然会发生段错误。同样的，在求和超过目标值同样的，该条链不再需要进行深入递归了，其判断如下：

1
2


if (sum == target)
    return 1;

以上为递归的主要结束条件，接下来是子集回溯算法的重点：

1
2
3


for (i = StartIndex; i < len; i++)
    if (recall(list, len, i + 1, sum + list[i], target))
        return 1;

我们最初函数的 StartIndex 参数为 0，也就是阶乘表的第一项数据，从该数据开始，我们进行分叉递归，每次递归的 StartIndex 就加 1，直至阶乘表每一项都生出字链。
而求和在 sum + list[i] 中完成，最初的 sum 值为 0，这样每一条子集链都能有最终的阶乘之和值。当每一条子链不断深入后遇到求和后与目标值相同就返回 1，当返回 1 回溯到最初的母函数跳出递归。否则一直遍历直至每一条都求和完返回 0。

最后的输出

显而易见，题意为该测试数据如果是任意阶乘之和就输出 Yes 否则输出 No，使用一组判断即可做到。

1
2
3
4


if (recall(list, j, 0, 0, target))
    printf("Yes\n");
else
    printf("No\n");

通过测试的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


#include <stdio.h>
#define M 1005

int recall(int list[], int len, int StartIndex, int sum, int target)
{
    int i;
    if (sum == target)
        return 1;
    if (StartIndex >= len || sum > target)
        return 0;
    for (i = StartIndex; i < len; i++)
        if (recall(list, len, i + 1, sum + list[i], target))
            return 1;
    return 0;
}

int main(int argc, char *argv[])
{
    int n, i, j;
    scanf("%d", &n);
    for (i = 0; i < n; i++)
    {
        int fac = 1, target;
        int list[M];
        scanf("%d", &target);
        for (j = 1; fac <= target; j++)
        {
            fac *= j;
            list[j - 1] = fac;
        }
        if (fac == target)
        {
            printf("Yes\n");
            break;
        }
        if (recall(list, j, 0, 0, target))
            printf("Yes\n");
        else
            printf("No\n");
    }
    return 0;
}