从简单一维迷宫学习 Q-Learning

引入

Q Learning 是强化学习的一种实现。
强化学习是让计算机从不懂到懂，通过不断尝试从错误中学习找到规律最终达到目的算法。通过奖励与惩罚的方式计算机可以不断摸索,可以说就是不断积累经验的过程。

我们首先引入一个一维迷宫。假设有 6 个块，其中一个块有宝藏。假设有一个计算机探险者，它不知道哪里有宝藏，只能选择向左或向右，要如何才能让探险者更快的找到宝藏呢？

1

O----T

这里 O 是探险者，T 是宝藏，- 是空白块。

我们使用 Python 实现这个过程。
代码放在 Github 仓库，需要的自取：
treasure_on_right.py

Q Learning 介绍

Q Learning 通过 Q 表存储每一块可能决策的收益。依据 Q 表来进行动作选择，并在每一次选择后计算收益以更新 Q 表。
通过 Q 表可以计算当前的最优策略。其的计算主要有两部分：

动作选择
更新 Q 表

对于 Q Learning 有一些量是需要介绍的：

动作(ACTIONS) ：动作是计算机可以做出的决策
理性值(EPSILON) ：对于动作选择中，作为随机或依据 Q 表的参考量
学习率(ALPHA) ：更新 Q 表时当前值的累加的权重
折扣因子(GAMMA) ：衡量未来奖励有多重要（有两个计算量分别是预期收益和实际收益，通过折扣因子表示两者对目标的权重）

动作选择算法

上文提到有理性值 EPSILON ，假设理想值为 0.9 说明有 90 % 的可能我们选择理性，而剩下的 10 % 就交给概率决定选择的动作。
当然，当在最初计算机没有任何经验的时候也会通过随机选择动作来打破僵局。

收益计算

当我们做出动作选择后，我们会运行并进行收益的计算。当实际收益与预期收益有差时，我们就更新 Q 表.
对于 Q 表更新值有：
$Q表新值 = Q表旧值 + 学习率 \times (实际收益 - 预期收益)$
显然当 $实际收益 - 预期收益 \neq 0$ 时会进行 Q 表更新。
对于收益计算简单来说有两种可能：下一步得到奖励或下一步没有奖励。

当下一步是终点

此时预期收益等于 Q 表当前值
实际收益等于 1，即得到奖励

当下一步不为终点

这个是一般情况，我们要继续计算收益。
预期收益还是 Q 表当前值。
$实际收益=奖励+未来预期最大收益 \times 折扣因子$
当实际收益和预期收益有差时更新 Q 表。

当上述对 Q Learning 基本阐述后，我们通过 python 实现的一维迷宫来实现 Q Learning 算法。

使用的 Python 库

1
2


import numpy as np
import pandas as pd

这里使用到两个数学数据分析相关的模块。
除此之外还有相关内置库 time os。

函数功能介绍

def rl() 这是整个程序的主体函数，在这里创建 Q 表，进行几轮的模拟最终得到不错的 Q 表
def build_q_table(n_states, actions) 初始化 Q 表
def choose_action(state, q_table) 对每一次移动做出抉择
def get_env_feedback(S, A) 得到下一步位置和是否获得奖励
def update_env(S, episode, step_counter) 更新环境，进行一些输出的绘制

RL 函数——程序主体

我们知道，该代码核心调用是 rl() 函数，展示一下该函数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


def rl():
    # main part of RL loop
    q_table = build_q_table(N_STATES, ACTIONS)
    for episode in range(MAX_EPISODES):
        step_counter = 0
        S = 0  # 位置
        is_terminated = False
        update_env(S, episode, step_counter)
        while not is_terminated:
            A = choose_action(S, q_table)
            q_predict = q_table.loc[S, A]
            S_, R = get_env_feedback(S, A)  # S_ 下一步的收益
            if S_ != "terminal":
                q_target = (
                    R + GAMMA * q_table.iloc[S_, :].max()
                )  # 实际收益=奖励+未来预期最大收益（非终点）
            else:
                q_target = R  # next state is terminal
                is_terminated = True  # terminate this episode

            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  #  更新 q 表
            S = S_  #  状态：往前走一步

            update_env(S, episode, step_counter + 1) # 绘制新的游戏界面
            step_counter += 1
            print("")
            print(q_table)
            time.sleep(0.5)
            # input("按下任意键后继续（需按回车）...")
            os.system("clear")
    return q_table

有一说一，pandas 模块的 DataFrame 数组确实挺好用的，就连打印都那么人类化！可谓难得。

q_table 在整个函数周期都存在，不会因为每一轮变化而重新初始化。 MAX_EPISODES 为训练的总回合数，在 for 循环里很明了。
又是几个变量说明：(有点烦)……

step_counter 计数器，计算每一回合的步数，可以从中看到强化学习的效果

S 初始位置(大写差评)

is_terminated 是否达到终点的标志，也就是 while 循环的结束条件，作用就是方便跳出 while 循环
后面还有一些比较"局部"的变量(python 可没有局部全局这种实际的说法)也就逐一介绍吧：

A 当前的行动

S_ 我们下一个状态，类型是个字符串(python 是这样的)。

R 奖励，这里只有 0 或 1

q_predict 预期收益

q_target 实际收益

下面逐行解释下 while 循环内单个回合的过程：

1

A = choose_action(S, q_table)

首先我们运行 choose_action(S, q_table) 获得下一步的行动。此时位置变量 S 还没有改变。将下一步行动先给变量 A

1

q_predict = q_table.loc[S, A]

读下一个位置的 Q 表获得预期收益。

1

S_, R = get_env_feedback(S, A)

获得下一步的位置索引和奖励

接下来是实际收益的计算：上文知道，我们需要判断下一步是否为终点来确定我们实际收益的计算方法整体代码如下：

1
2
3
4
5
6
7


if S_ != "terminal":
    q_target = (
        R + GAMMA * q_table.iloc[S_, :].max()
    )  # 实际收益=奖励+未来预期最大收益（非终点）
else:
    q_target = R  # next state is terminal
    is_terminated = True  # terminate this episode

需要简单提下 S_ 变量到底会存储啥。
S_ 可能会有两种数据类型的可能（天哪，也就只有 python 可以这样做了！🥺）int 或者 str
在 get_env_feedback(S, A) 里，如果下一步是终点直接返回 "terminal" 这个字符串，否则就返回下一步的位置。(python 字符串类型太好用了不是)

这里比较抽象的是 q_table.iloc[S_, :].max() ，对于 python 有非常多语法糖，一般来说在 python : 符号用于切片，而单独的 : 就是全部数据。
iloc() 方法用于根据索引访问数据，然后通过链式调用给 max() 取出两个数据的最大值。这里体现了贪心思想。

整个条件判断就是上文讲的实际收益。

1

q_table.loc[S, A] += ALPHA * (q_target - q_predict)  #  更新 q 表

通过增量式的计算更新 Q 表。

1

S = S_  #  状态：往前走一步

实际更新位置变量

1
2
3
4
5
6
7


update_env(S, episode, step_counter + 1) # 绘制新的游戏界面
step_counter += 1
print("")
print(q_table)
time.sleep(0.5)
# input("按下任意键后继续（需按回车）...")
os.system("clear")

一些自己补充用于更好展现 Q 表更新的代码。不解释了（

1

return q_table

返回最终的 Q 表

至此，rl 函数就解释完了。整个 Q Learning 核心逻辑也基本解释差不多了。

`choose_action(state, q_table)` 函数——动作选择函数

1
2
3
4
5
6
7
8
9


def choose_action(state, q_table):
    # This is how to choose an action
    state_actions = q_table.iloc[state, :]  # 将该位置的左右权数全部取出
    if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):  # 非理性状态
        action_name = np.random.choice(ACTIONS)
    else:  # 理性状态
        action_name = state_actions.idxmax()  # 取最大值作为 action 名字
        # 返回方向（id)
    return action_name

返回值 action_name 是 ACTIONS 列表里的一个值，应该是 str 类型。
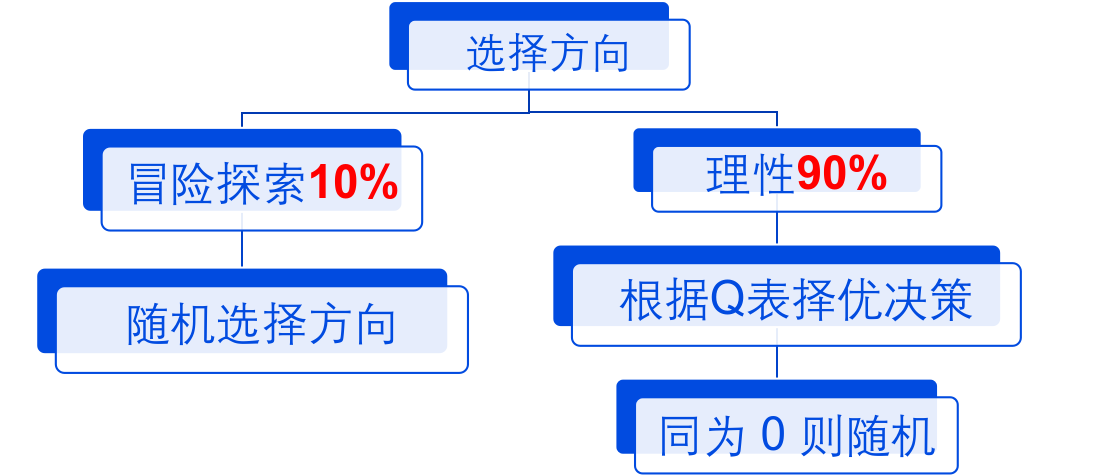
当 EPSILON = 0.9 对于动作选择函数有:

1

state_actions = q_table.iloc[state, :]  # 将该位置的左右权数全部取出

这里的 state_actions 保存了两个值：Q 表该元素的 left 和 right。

对于动作选择函数主要区分是否选择冒险探索的判断条件:

1

if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):  # 非理性状态

有些许抽象(其实是太抽象了)
numpy.random.uniform() 是生成一个随机数，默认没有参数时生成随机数范围为 [0, 1)。
显然当生成的随机数大于 EPSILON 的可能性为 0.1 符合冒险探索的可能
除此之外，当该块的 Q 表左右两个值都为 0，也就是还没有得到收益时候也应该进行冒险探索，条件为 ((state_actions == 0).all()) 也蛮不好理解的……
(state_actions == 0) 是布尔值，传参到 all() 方法就是 state_actions 两个参数都为 0 时为真（python 面向对象还在发挥）。这样就能判断出在最初没有实际收益时的情况。

让我们深入去了解（这个函数逻辑好理解，就是用了很多抽象的 python 语法）

当 if 成立也就是进行冒险探索时，我们执行该函数：

1

action_name = np.random.choice(ACTIONS)

它随机从 ACTIONS 中选取一个值给 action_name 作为我们下一步行动的方向
2. 当 if 不成立，执行 else 语句进入理性选择

1

action_name = state_actions.idxmax()  # 取最大值作为 action 名字

直接选择最大值的索引标签为返回值。在初始化时 pandas.DataFrame 数据类型可以指定索引标签（抽象++）。
至此，动作选择算法函数就差不多了。

`build_q_table(n_states, actions)` Q 表的初始化

Q 表(q_table) 用的是 pandas 模块的 DataFrame 数据类型(抽象++)。

1
2
3
4
5
6
7


def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),  # q_table initial values
        columns=actions,  # actions's name
    )
    # print(table)    # show table
    return table

DataFrame 数据类型太强大了(强大到我都看晕了)。这里给出它的构造方法。

1

pandas.DataFrame(data=None, index=None, columns=None, dtype=None, copy=False)

我们这里只用到了两个参数，第一个为默认第一个参数 data，直接用 numpy 初始化一个 n_states 行 actions 列的二维数组。
然后第二个参数是 columns (不是默认第二个参数。)，将列的索引标签写为 actions 值。
最后返回创建的表格。

`get_env_feedback(S, A)` 获取下一步的位置和奖励

这个函数比较简单，没有那么多抽象的语法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


def get_env_feedback(S, A):
    # This is how agent will interact with the environment
    # 下一步的位置和奖励
    if A == "right":  # move right
        if S == N_STATES - 2:  # terminate
            S_ = "terminal"
            R = 1  # 奖励
        else:
            S_ = S + 1
            R = 0
    else:  # move left
        R = 0
        if S == 0:
            S_ = S  # reach the wall
        else:
            S_ = S - 1
    return S_, R

形参 A 其实在 rl() 是通过 choose_action 选择的动作。这里通过判断下一步的动作获得下一步的位置和奖励。如果此时下一步位置为右，而且当前位置在奖励左边，则可以判断出奖励为 1。这个函数其实仔细研究下就能懂。

这里要特判在第一个位置也就是 S = 0 时是不能往右走的。
注意的是这里的返回：return S_, R 返回了两个参数，在调用也要用两个参数接收，在 rl() 函数中接收。

`update_env(S, episode, step_counter)` 输出信息

这个函数输出了当前迷宫的情况以及一些位置的

1

env_list = ["-"] * (N_STATES - 1) + ["T"]

先初始化一个迷宫图，这时候没有探索者，特判如果已经达到了奖励位置则输出回合数和和该回合数的步数。

1
2
3
4
5


if S == "terminal":
    interaction = "Episode %s: total_steps = %s" % (episode + 1, step_counter)
    print("\r{}".format(interaction), end="")
    time.sleep(2)
    print("\r                                ", end="")

这里 print() 格式化，同时把默认后置换行取消掉。
如果没有在奖励位置则将位置所代表的索引字符串表替换成 o 代表探索者。
后面七七八八的不详细说了，都差不多。

其他代码

1

np.random.seed(2)  # reproducible

代码开始的 numpy 随机数种子

1
2
3
4


if __name__ == "__main__":
    q_table = rl()
    print("\r\nQ-table:\n")
    print(q_table)

程序入口

实际示例

第一回合结束:

1
2
3
4
5
6
7
8
9


o----T
   left  right
0   0.0    0.0
1   0.0    0.0
2   0.0    0.0
3   0.0    0.0
4   0.0    0.1
5   0.0    0.0
Episode 1: total_steps = 38

第二回合结束：

1
2
3
4
5
6
7
8
9


-o---T
   left  right
0   0.0  0.000
1   0.0  0.000
2   0.0  0.000
3   0.0  0.009
4   0.0  0.190
5   0.0  0.000
Episode 2: total_steps = 22

第四回合结束：

1
2
3
4
5
6
7
8
9


----oT
   left     right
0   0.0  0.000000
1   0.0  0.000073
2   0.0  0.002997
3   0.0  0.047070
4   0.0  0.271000
5   0.0  0.000000
Episode 4: total_steps = 5

到这时候只需要 5 步就能走到了
最后:

1
2
3
4
5
6
7
8
9


Q-table:

       left     right
0  0.000000  0.004320
1  0.000000  0.025005
2  0.000030  0.111241
3  0.000000  0.368750
4  0.027621  0.745813
5  0.000000  0.000000

到最后基本上可以一路向右直接走到终点不带犹豫的。