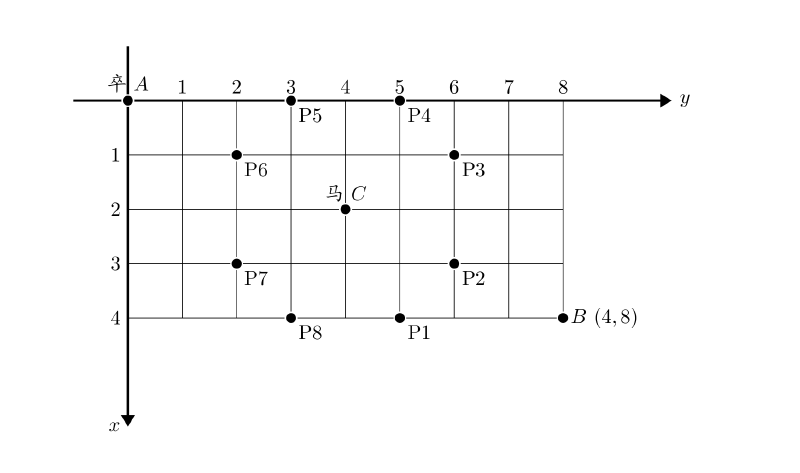
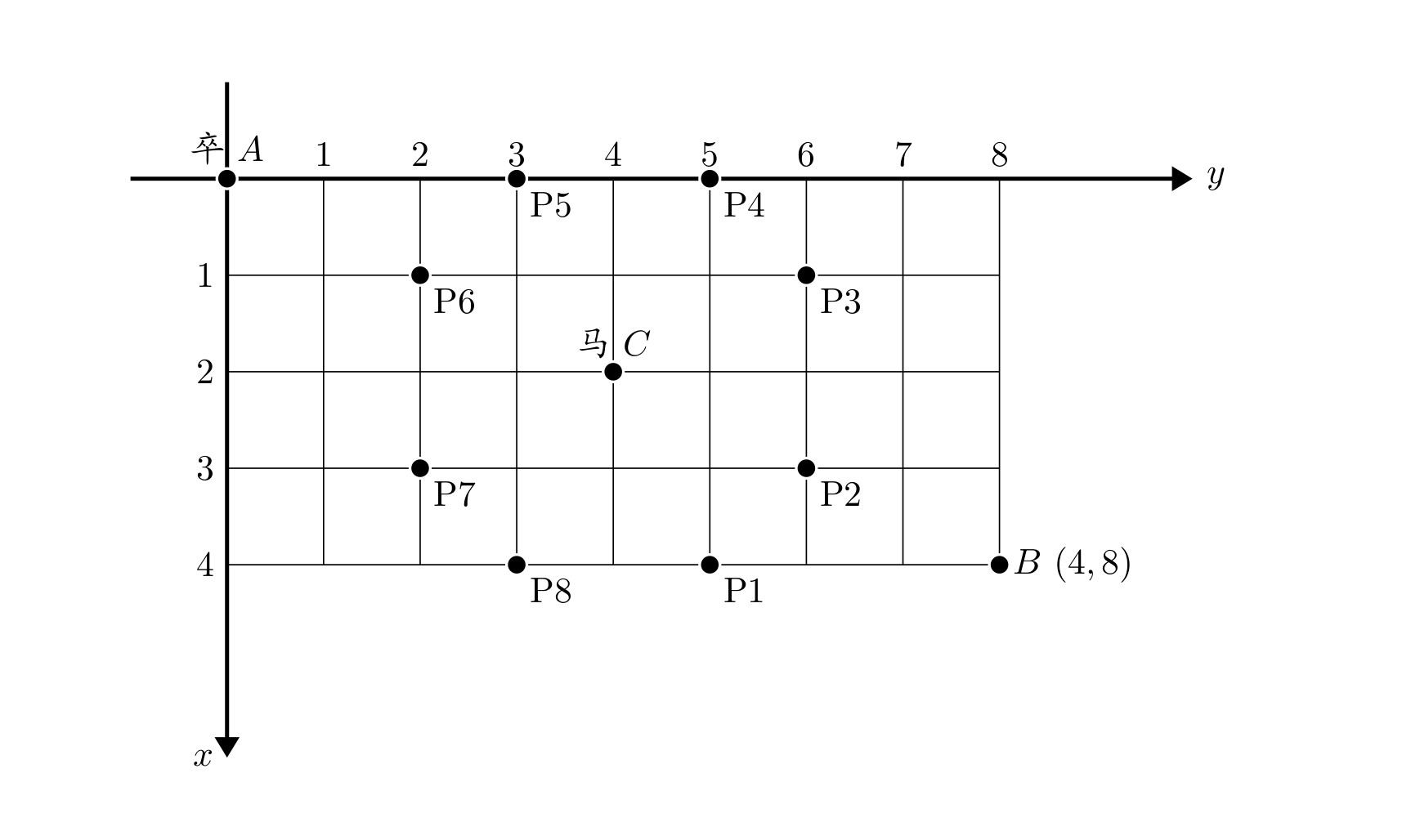
题目
经典洛谷第 3 题……
传送门
其实是入门动态规划题，当然使用回溯递归也是能写的。
动态规划
动态规划可以说就是用正向的递推方式通过前一子问题一步步求解最终的答案。其将原问题分解为相对简单的子问题，先求解子问题再由子问题的解而得到原问题的解。
对于动态规划，一般在求解过程会出现重叠的子问题，此时用递归分治就会很浪费时间，显然将重叠子问题保存在子问题可以避免大量的重复计算。
动态规划一个简单例子是斐波那契数列这里贴上 python 实现，不展开：
1
2
3
4
5
6
7
8
|
def fib(n: int) -> int:
dp = [0 for _ in range(0, n + 1)]
dp[0] = 1
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
|
这里的 dp[i] = dp[i - 1] + dp[i - 2] 就是状态转移方程，是动态规划比较核心的逻辑！
过河卒题解
思路
对于过河卒，还是有一定的思维量的(其实对于我来说还真琢磨了半天)。最开始可能会被整体模拟量吓到，但是细究下来可以发现对于其的每个点(x, y) 的走法 都可以由 (x-1, y) 、(x, y-1) 两点走法相加得到。而且，我们可以知道最初卒的位置只有 1 种走法。如果不考虑马的话可作如下表：
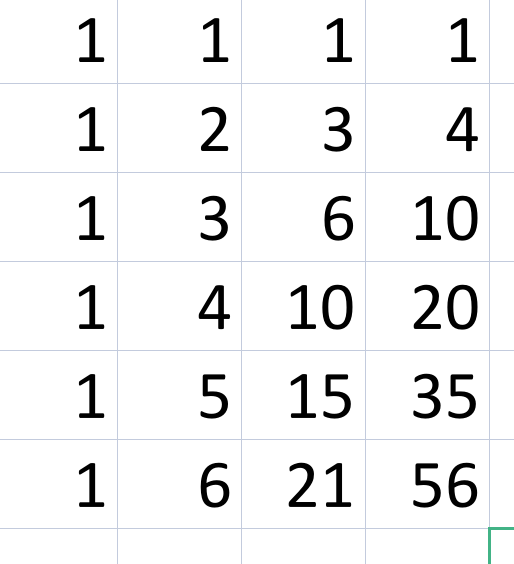但是，当我们考虑了马，在假设我们在 (x-1, y) 上是马可能的位置，卒不能过，该点的可能路径就归零。对于此，在其之后的点向后是无法得到路径的，也就是 + 0。
受到马影响的位置一共有 9 种情况，可以通过二维数组列举出来在之后进行遍历判断：
1
|
int jumpOffset[9][2] = {{0, 0}, {-1, 2}, {-2, 1}, {1, 2}, {2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
|
顺便把前面一堆变量声明、输入处理放出来：
变量与输入处理
1
2
3
4
5
6
7
8
9
|
int a, b, x, y;
int tempX, tempY;
int ResX, ResY;
int jumpOffset[9][2] = {{0, 0}, {-1, 2}, {-2, 1}, {1, 2}, {2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
scanf("%d%d%d%d", &a, &b, &x, &y);
int horsePos[a + 1][b + 1];
long long board[a + 1][b + 1];
memset(board, 0, sizeof(board));
memset(horsePos, 0, sizeof(horsePos));
|
a b 为终点的坐标， x y 为马的坐标。
tempX tempY 后面存储马的可能跳跃点。
后面从终点坐标对棋盘数组进行创建，同时使用 memset 初始化数组为 0。
horsePos 是马和马可跳跃点的坐标表示，在后续需要用到。
遍历马的控制点
接下来就是通过 jumpOffset 数组遍历得到马可跳跃点存储到 horsePos。如果该点是马的跳跃点，就标记为 1,在后面进行遍历动态规划时候，遇到马的 horsePos 为 1 的点就跳跃不运算状态转移方程，此时该点为 0，在之后涉及到该点的状态转移方程 +0 说明没有路径通过，该点无法通过。
1
2
3
4
5
6
7
|
for (int i = 0; i < 9; i++)
{
tempX = x + jumpOffset[i][0];
tempY = y + jumpOffset[i][1];
if (tempX >= 0 && tempX <= a && tempY >= 0 && tempY <= b)
horsePos[tempX][tempY] = 1;
}
|
状态转移方程
对于任意一点$f_{(x, y)}$，有:
$f_{(x, y)}=f_{(x-1, y)}+f_{(x, y-1)}$
同时再考虑边界问题后可以得到过河卒的动态规划思路了。
初始条件
首先可以确定 $f_{f(0, 0)}$ 是卒的位置，它一定有 1 条路径，有如下代码：
但是洛谷的深入浅出给的代码是：
1
|
board[0][0] = 1 - horsePos[0][0];
|
它考虑了原点是马的控制点，此时所有路径应该都是无效的，不过两者都是可以通过测试的。
遍历格子套入方程
以两层嵌套循环遍历所有格子对每个格子分 x, y 两个方向累加即可：
1
2
3
4
5
6
7
8
9
10
11
12
|
for ( int i = 0; i <= a; i++)
{
for (int j = 0; j <= b; j++)
{
if (horsePos[i][j])
continue;
if (i != 0)
board[i][j] += board[i - 1][j];
if (j != 0)
board[i][j] += board[i][j - 1];
}
}
|
可以发现，当遍历的点是马的控制点就跳过这次循环。整体思路很清晰，通过判断 i!=0 与 j!=0 防止运算时越界。
最终答案
在遍历到最后可以发现，board[a][b] 位置即为我们需要的答案：
1
|
printf("%lld", board[a][b]);
|
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <cstdio>
#include <cstring>
int main(int argc, char *argv[])
{
int a, b, x, y;
int tempX, tempY;
int jumpOffset[9][2] = {{0, 0}, {-1, 2}, {-2, 1}, {1, 2}, {2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
scanf("%d%d%d%d", &a, &b, &x, &y);
int horsePos[a + 1][b + 1];
long long board[a + 1][b + 1];
memset(board, 0, sizeof(board));
memset(horsePos, 0, sizeof(horsePos));
for (int i = 0; i < 9; i++)
{
tempX = x + jumpOffset[i][0];
tempY = y + jumpOffset[i][1];
if (tempX >= 0 && tempX <= a && tempY >= 0 && tempY <= b)
horsePos[tempX][tempY] = 1;
}
board[0][0] = 1 - horsePos[0][0];
for ( int i = 0; i <= a; i++)
{
for (int j = 0; j <= b; j++)
{
if (horsePos[i][j])
continue;
if (i != 0)
board[i][j] += board[i - 1][j];
if (j != 0)
board[i][j] += board[i][j - 1];
}
}
printf("%lld", board[a][b]);
return 0;
}
|
参考资料
- 算法通关手册 8.1 动态规划基础
- 洛谷 深入浅出程序设计竞赛（基础篇） 高等教育出版社
