算法

C++算法-筛选素数

很多算法题与素数相关，对于素数需要掌握诸多内容并灵活应用。筛选素数是很重要的。
素数的定义在 Wikipedia 上为: 大于 1 的自然数中，除了 1 和该数本身外无法被其他自然数整除的数，同时也可以被定义为只有 1 和它本身两个正因数的数。
与素数相反的数叫合数。

判断素数

要判断 $n$ 是否为素数，基于定义我们可以写如如下函数:

1
2
3
4
5
6

bool isPrime(int n){
    for (int i = 2; i < n; ++i){
        if (n % i == 0) return false;
    }
    return true;
}

但有没有更好的方法进行优化呢？
实际上如果我们要求 $n$ 是否为一个素数，我们要判断除了 $1\times n=n$之外还有别的正整数相乘可以等于 $n$。
对于合数来说，有 $a\times b=n$($1<a\leq b<n$)。 若合数$n=12$要验证是否为素数:
$2\times 6=12$
$3\times 4=12$
$\sqrt{12}\times\sqrt{12}=12$
$4\times 3=12$
$6\times 2=12$
以 $\sqrt{12}\times\sqrt{12}=12$ 为节点观察：
12%2=6 和 12%6=2 是完全一样的，只需要判断前者即可。这是因子的对称性。
如果使用原先的算法素数就要遍历完 $2\sim n-1$这些数，但在 $i=\sqrt{n}$后，实质上发生了没有必要的重复。因而可以将循环条件中的i<n替换为i < sqrt(n)或 i * i < n 。显然后者更好些，因为 sqrt() 的参数和返回值的类型都是 double，进行隐性类型转换总归是要避免的。

1
2
3
4
5
6

bool isPrime(int n) {
    for (int i = 2; i * i <= n; i++) {
        if (i % n == 0) return false;
    }
    return true;
}

这样的函数将复杂度从 $O(n)$ 减小到 $O(\sqrt n)$，在大数下会有更换的性能。

求素数个数

这篇文章的最终目的是要筛选小于等于 n 的素数或返回素数或返回个数。
最简单的当然是一个个去判断进行暴力列举了。

暴力列举法

采用上文的 bool isPrime(int n) 函数，计算小于等于 n 有多少素数暴力算法如下:

1
2
3
4
5
6
7

int countPrimes(int n){
    int count = 0;
    for (int i = 1;i< n;i++){
        if (isPrime(i)) count++;
    }
    return count;
}

暴力解法使用优化过的素数判断函数最后的复杂度为 $O(n\sqrt n)$ 效率低下。

埃拉托斯特尼筛法

如果要求的数很大，暴力法效率就很低了。但是当数大了，可以发现如果一个数是素数，那么它的整数倍必定是合数。
这可是一个巨大的发现，由此越大的范围可以节省判断次数就越多，效率就越高。我们只需要维护一个列表，将每个素数的整数倍标记为合数。在遍历完后的没有被标记的数就是素数了。 在 WikiPedia 有不错的动图:

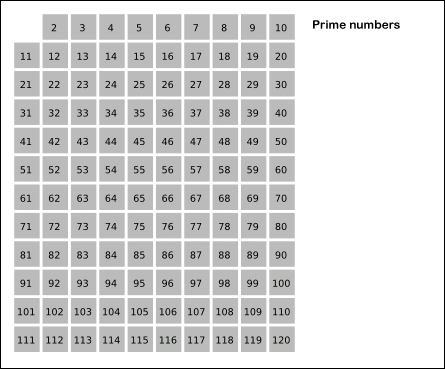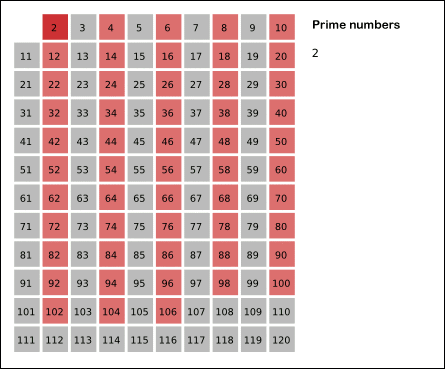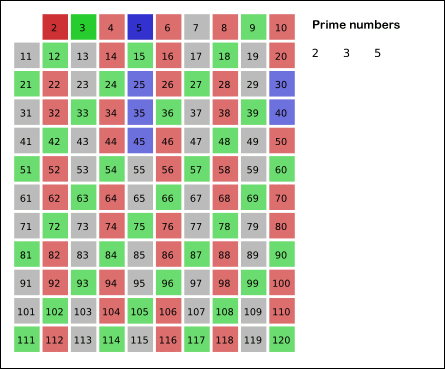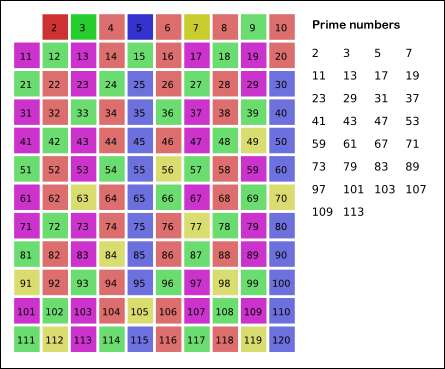
注:最后要得到的是 $[2, n]$ 区间内的素数。

我写的返回包含该区间内所有素数列表的函数，要求素数数使用 size() 方法或在内加一个计数变量即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

vector<int> countPrimes(int n) {
    vector<bool> isPrimes(n + 1, true);
    vector<int> Primes;

    for (int i = 2; i * i < n + 1; ++i) {
        if (isPrime(i)) {
            for (int j = i * i; j < n + 1; j += i) {
                isPrimes[j] = false;
            }
        }
    }

    for (int i = 2; i <= n; ++i) {
        if (isPrimes[i]) Primes.emplace_back(i);
    }

    return Primes;
}

这里使用布尔列表来标记是否为素数，长度为 n + 1，因为在后面要用索引代表数字，显然列表的索为 $0\sim n-1$。如果 $n$ 为素数最后是取不到的。
第一块循环第一层使用 i * i < n + 1 作为循环条件同样是根据因子的对称性取 $\sqrt{n}$，我们要得到合数，不需要考虑 $\sqrt{n}$ 之后的数，后面会考虑到。
对 $[2, \sqrt{n})$之间的数进行素数判断，如果是素数那么进入下一层循环。
显然我们知道素数的整数倍一定是合数，对其进行标记就行。注意:我们标记合数不需要从 $2i$ 开始标记，可以从 $i^2$ 开始。

因为较 $i^2$ 更小的 $i$ 的倍数一定拥有更小的素数为其因数。使用 $i^2$ 可以避免重复标记。

所以这一层循环从 i * i 开始。直到 $n+1$ 结束。对布尔列表 isPrimes 的 j 项取 false。
这样， isPrimes 每个元素的值就对应着其索引值是否为素数。
接下来要遍历一遍 isPrime 把结果为 true 元素对应的索引值添加到 Primes 列表中。而后就能返回了。

埃拉托斯特尼筛法的时间复杂度为 $O(n\log {\log {n}})$。

参考资料

  1. WikiPedia - 素数
  2. labuladong 的算法笔记 - 如何高效寻找素数
  3. WikiPedia - 埃拉托斯特尼筛法
  4. OI Wiki - 筛法
萌ICP备20241614号