Featured image of post 数据结构 栈 初步
数据结构

数据结构 栈 初步

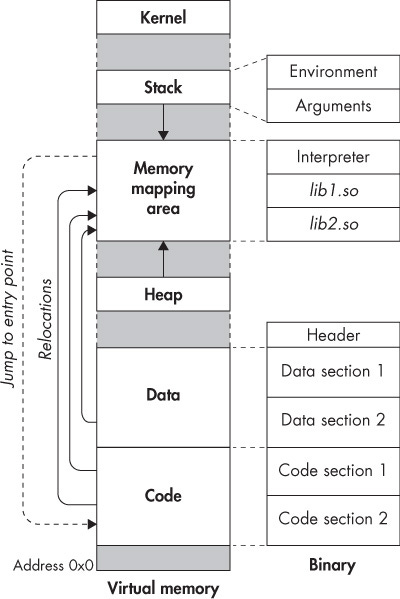
我经常在各处地方看到 “堆栈溢出” 。在计算机的各处地方看到栈的影子，特别是当我了解到 Linux 可执行文件的结构之后，才初窥栈的强大。到现在，开始学习数据结构，也算是略有参透一些，本文就简单讲讲栈这个数据结构。

引入：Linux 可执行文件下的栈

Linux ELF 结构
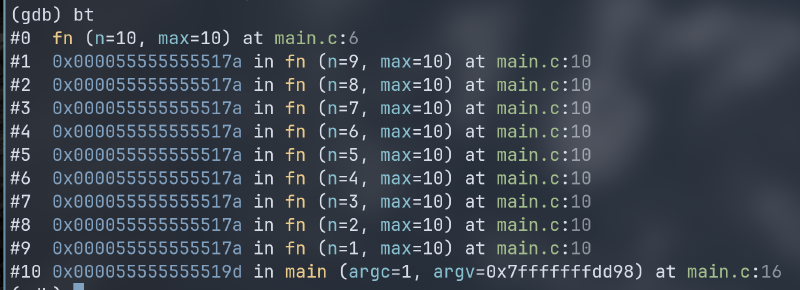
在其的可执行性文件中有一块区域作为栈，用于存储程序运行时函数的局部变量、参数和返回值。实际上在程序中函数的调用嵌套和入栈出栈是相似的。在 gdb 中使用 bt 可以回溯显示当前调试程序的调用栈，每个调用栈元素都存储着函数的数据，比如我们写如下递归程序：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

#include <stdio.h>

void fn(int n, int max)
{
    if (n == max)
        return;
    else
    {
        printf("%d\n", n);
        fn(n + 1, max);
    }
}

int main(int argc, char *argv[])
{
    fn(1, 10);
    return 0;
}

我们编译时加上 -g 调试参数，之后进入 gdb ，将 第 6 行的 return 加上断点后输入 r 运行，程序在 return 行停下，通过 bt 查看当前调用栈，输出如下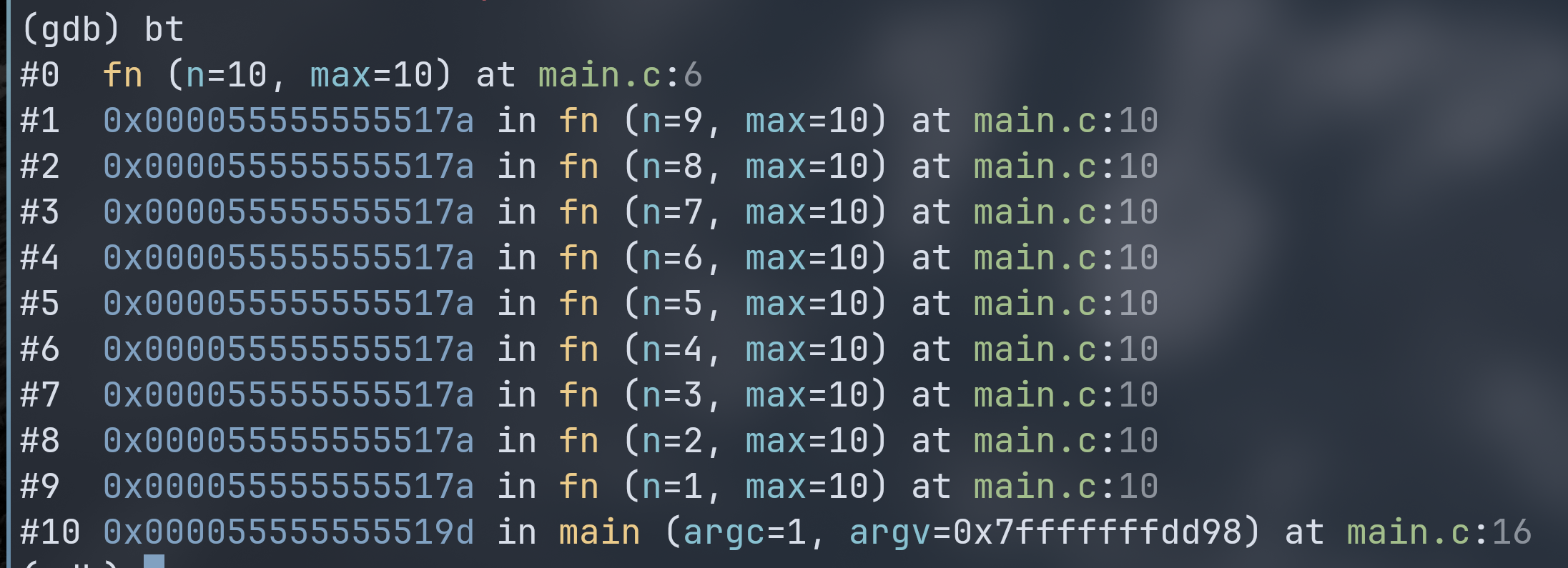： 可见通过递归不断嵌套调用 fn 函数，该函数与其子函数不断入栈。
我们再修改程序，将入栈深度加大，同时通过 ulimit 缩小程序的栈空间：
将 main() 下的 fn 修改为：

1

fn(1, 10000);

而后通过 ulimit 修改程序的栈空间为 300 kb :

1

ulimit -s 300

再次编译程序并运行………… 然后：
BOOM!!!

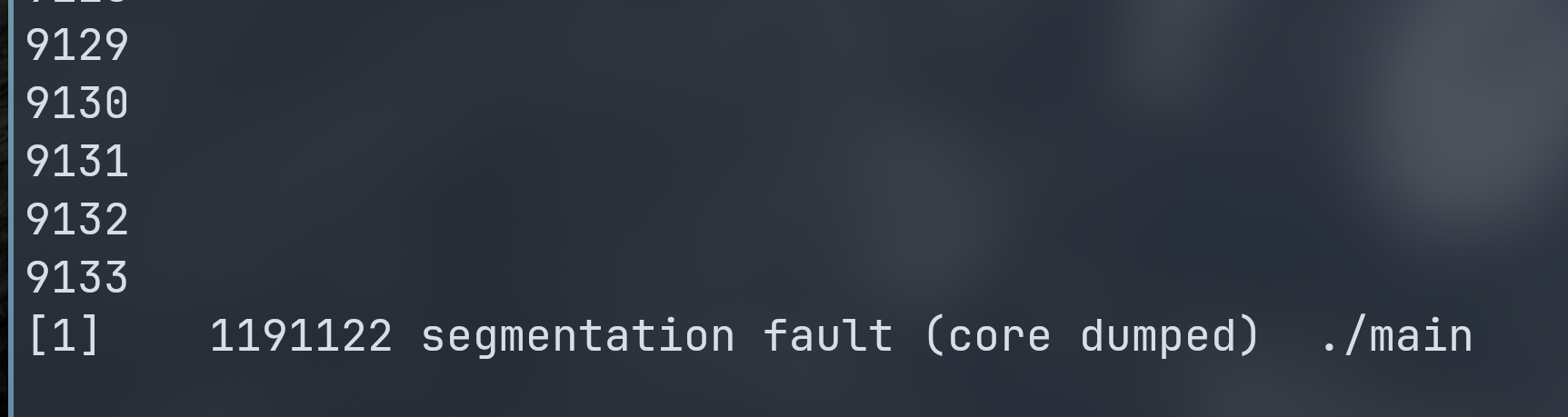
当程序打印出 9133 后，程序出现段错误被强制退出，这便是臭名昭著的堆栈溢出。
是的，栈是一块有限的空间。当我们缩小栈的空间，随着程序不断递归，栈内元素不断增多，直到最后超过 300 kb，最后就溢出了，程序错误，并被操作系统强制结束。

栈可以通过数组的结构化限制实现：

实现一个栈结构

这里作一个以连续内存空间为基础的顺序栈。
初始化声明一些东西，通过类型重定义使得数据结构更为通用。

1
2
3
4
5
6
7

#include <cstdio>
#include <stdlib.h>

#define initSize 20 // 栈空间初始大小

typedef int SElemType; // 栈元素类型
typedef int DataType;

实际栈结构的定义：

1
2
3
4
5
6
7

// 顺序栈结构定义
typedef struct
{
    SElemType *elem; // 栈元素存储数组
    int maxSize;     // 栈空间最大容量
    int top;         // 栈顶指针（下标）
} SeqStack;

因为栈本身的限制，我们只需要获得其的顶端指针即可。
至于为什么它的指针是整形呢，这就和数组下标有关了。数组下标实质可以等价于指针操作，比如：A[2] 等价于 *(A+2)。而这个 2 便有了一种指针的样子。

在构建好栈结构之后，需要编写函数对其初始化：

  • 为元素数组分配空间
  • 为最大空间赋值
  • 为栈顶指针赋初始值

此时是栈为空。因为下标从 0 开始，所以栈空时候栈顶指针top为 -1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// 建立一个最大尺寸为 initSize 的空栈，若分配不成功则进行错误处理
void InitStack(SeqStack &S)
{
    S.elem = (SElemType *)malloc(initSize * sizeof(SElemType)); // 创建栈空间
    if (S.elem == NULL)
    {
        printf("存储分配失败!\n");
        exit(1);
    }
    S.maxSize = initSize;
    S.top = -1;
}

栈的操作

栈的操作主要分为出栈和入栈。这也体现了栈的优势。栈是限定了存取位置的线性表。可以称栈为后进先出的线性表(LIFO)。
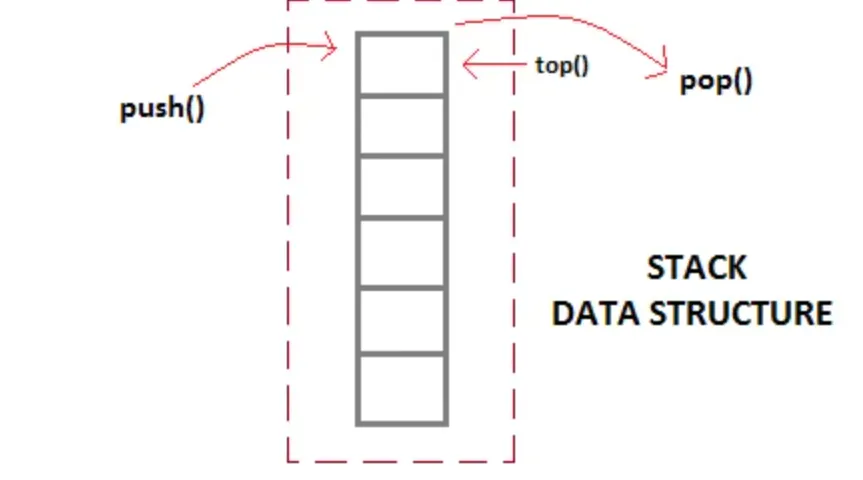可以把栈看出一个仅一端开口的数组，我们进行入栈出栈的数据都是在开口那一端进行，也只能访问最顶上的数据，也就是栈顶，这也是为什么我们需要一个栈顶指针。

入栈

1
2
3
4
5
6
7
8

// 入栈操作：若栈不满，则将元素 x 插入栈顶，函数返回 1；否则栈溢出，函数返回 0
int Push(SeqStack &S, DataType x)
{
    if (S.top == S.maxSize - 1) // 栈满则溢出处理
        return 0;
    S.elem[++S.top] = x; // 栈顶指针先加 1 ，再进栈
    return 1;
}

先给函数，首先需要判断是否栈满，如果栈满就无法执行入栈操作，否则会出现栈溢出（正如上文提到的那样）。
对 .elem 栈顶进行赋值操作。这里使用 ++S.top 在自增栈顶指针后将其的值指向数组中的位置进行赋值，是个很漂亮的操作！

出栈

1
2
3
4
5
6
7
8
9

// 出栈：若栈不空则哈暗示通过引用参数 x 返回栈顶元素值，栈顶指针退 1，函数返回 1
// 否则函数返回 0。
int Pop(SeqStack &S, SElemType &x)
{
    if (S.top == -1)
        return 0;
    x = S.elem[S.top--];
    return 1;
}

同样的，要判断是否栈空。栈空自然是无法再出栈的。

1

x = S.elem[S.top--];

这里将出栈的元素传递给引用参数 x 。使得我们可以在调用后通过 x 来访问出栈的数据。
和入栈有异曲同工之妙的是：

1

x = S.elem[S.top--];

在给 x 赋值的同时对栈顶自减，此时即使原栈顶还存在数据但在栈中已经不可访问，所以无关紧要直接 S.top-- 后即可，之后若需要再覆写。

栈的访问

对栈的访问只限于栈顶数据，同时，我们还可以通过结构体存储的信息判断栈空和栈满。

读取栈顶数据

我们可以直接读取栈顶数据而不需要进行退栈操作：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// 读取栈顶元素值；若栈不空函数返回栈顶元素的值且函数返回 1，否则函数返回 0
int GetTop(SeqStack &S, SElemType &x)
{
    // 判断是否栈空，栈空返回 0
    if (S.top == -1)
        return 0;
    // 返回栈顶元素的值
    x = S.elem[S.top];
    return 1;
}

如果栈空，是没有数据可访问的。需要进行判断。

判断栈空栈满

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

// 判断是否栈空，栈空返回 1，否则返回 0
int StackEmpty(SeqStack &S)
{
    return S.top == -1;
}

// 判断是否栈满，栈满返回 1，否则返回 0
int StackFull(SeqStack &S)
{
    return S.top == S.maxSize;
}

通过逻辑运算进行返回是个不错的选择，因为栈结构已经包含了 top 和 maxSize 数据，对其进行判断即可。
先前我们规定栈空时 top 为 -1，所以我们只需要判断 top 是否为 -1 即可知道是否栈空。
同理，当栈满时 top 是等于 maxSize 的，对其作相等性判断即可判断是否栈满。

返回栈的长度

1
2
3
4
5

// 函数返回栈 S 的长度
int StackSize(SeqStack &S)
{
    return S.top + 1;
}

由于我们栈是从 0 开始存放的，所以实际长度要比栈顶指针得到的还要 +1。

参考资料

  1. 殷人昆 数据结构（C 语言版）（第二版） 清华大学出版社
萌ICP备20241614号